科學計算語言的定義
在「約維安計畫:NumPy」我們認識了 NumPy 模組給予的 ndarray 資料結構,儲存同質資料的 n 維數值陣列提供了與 Python 內建資料結構截然不同的功能面向,前者專注於計算效率、後者則著重於儲存彈性。事實上 NumPy 模組被命名為 Numeric Python(or Numerical Python) 就意味著這是一個位 Python 實踐數值計算的模組,也是科學計算的入門磚,簡而言之,假使我們提出一個問題:究竟是什麼原因能夠讓 Python 從「泛用程式語言」搖身一變為「科學計算語言」呢?答案呼之欲出:NumPy 模組。
看到這裡讀者不免感到納悶,怎麼說 Python 不是「科學計算語言」呢?Python 不是數據分析、資料科學與機器學習的首選程式語言嗎?這時我們應該要探究「科學計算語言」的廣義或嚴格定義:
廣義而言,科學計算語言指的是被多數科學研究者用於計算、數學或科學程式語言,因此,C/C++ 和 Python 可以被認為是廣義的科學計算語言。
嚴格定義而言,科學計算語言是為數學公式計算以及矩陣計算而設計、優化的程式語言,這類型的語言不僅要具備能夠相關的模組與套件,還要具備數學與科學計算的語法,例如,C/C++ 和 Python 都沒有內建的矩陣資料結構類別,亦沒有內建的矩陣運算函數、運算符號,這些功能必須仰賴標準或者第三方模組與套件提供。因此在嚴格定義下 C/C++ 和 Python 並不是科學計算語言,符合嚴格定義的科學計算語言包括 ALGOL、APL、Fortran、J、Julia、Maple、MATLAB 和 R。
來源:https://en.wikipedia.org/wiki/Scientific_programming_language
如何關聯 ndarray 與數學
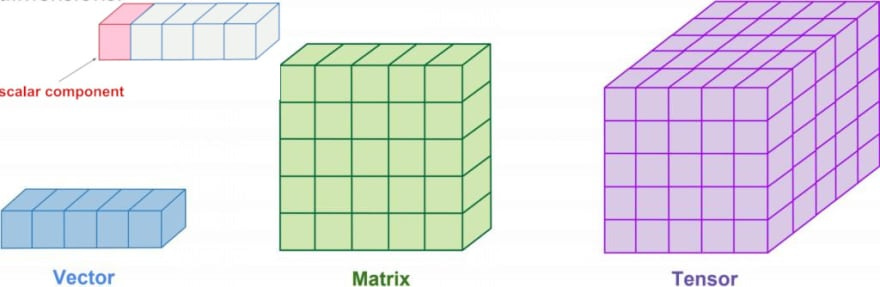
ndarray 資料結構類型的設計和數學對待資料維度的概念一致,在數學上我們有純量、向量、矩陣與張量分別去描述零維、一維、二維與 n 維的資料,在 ndarray 的建立上,同樣也有零維陣列、一維陣列、二維陣列與 n 維陣列,我們可以用一張示意圖來暸解資料維度:
矩陣運算
矩陣是一個由 m 列(row)n 欄(column)元素所組成的二維陣列,其中一個重要用途是解線性方程組,也常見於數值計算、統計分析與電腦科學等,在 NumPy 模組中我們就用二維的 ndarray 來建立與操作矩陣,因此像是列向量(row-vector)或者欄向量(column-vector)雖然在命名中是向量,我們仍會以外型 (1, n) 或者 (m, 1) 的二維陣列來對應,藉此確保維度的一致性。
u = np.array([5, 6, 7, 8]).reshape(-1, 1)
v = np.array([5, 6, 7, 8]).reshape(-1, 1)ndarray 與 list 的其中一個差異處就在於元素對應運算(Element-wise),有時亦稱為向量化運算(Vectorization),我們可以讓 ndarray 和一個純量直接運算。
print(u * 5)
print(v * 6)常見的矩陣處理技巧為轉置(Transpose),能夠將外型 (m, n) 的矩陣轉換為外型 (n, m),這樣能使得位於 m 列 n 欄的元素,更動到 n 列 m 欄的位置。我們可以使用 np.transpose() 函數或者 ndarray 的 T 屬性。
A = np.arange(1, 7).reshape(2, 3)
transpose_A = np.transpose(A)
A_T = A.T
print(A)
print(transpose_A)
print(A_T)列向量或欄向量的「相乘運算」除了元素對應運算外還有矩陣相乘,也就是所謂的乘積運算(Dot product),相乘的前提是左側向量的欄數和右側向量的列數必須相等。
我們可以使用 np.dot() 函數或者 ndarray 的 dot() 方法來進行欄向量相乘。
print(np.dot(u.T, v))
print(u.dot(v.T))同樣的道理,矩陣相乘的前提也是左側矩陣的欄數和右側矩陣的列數必須相等。
A = np.arange(1, 7).reshape(2, 3)
B = np.arange(1, 7).reshape(3, 2)
print(A.dot(B))利用 np.eye() 函數建立單位矩陣(Identity matrix),單位矩陣是一個方矩陣(意即列數與欄數相等),其對角線上的元素都是 1。
I_22 = np.eye(2)
I_33 = np.eye(3)
I_44 = np.eye(4)
print(I_22)
print(I_33)
print(I_44)單位矩陣在矩陣運算中的作用與常數 1 在代數運算中的作用相似,在代數中變數與其倒數相乘可以得到常數 1,解此來求解方程式,例如在解下列代數方程式的時候我們會將等號兩邊乘上 a 的倒數來求解。
面對矩陣代數的時候,矩陣與其反矩陣相乘可以得到單位矩陣,因此在解下列矩陣代數方程式的時候,是將等號兩邊乘上 A 的反矩陣來求解,我們可以使用 np.linalg.inv() 函數計算 A 的反矩陣。
以下列的線性方程組為例:
A = np.array([1, 3, 1, 2]).reshape(2, 2)
B = np.array([5, 3]).reshape(2, 1)
inv_A = np.linalg.inv(A)
x = inv_A.dot(B)
print(x)入門矩陣運算之後,我們就能夠在未來的電子報中透過 ndarray 運算認識機器學習的資料預處理與模型訓練,這週也是我第一次使用了 Substack 的 LaTex 功能,非常開心!在認識了 NumPy 與矩陣運算之後,第三十四週約維安計畫來到尾聲,希望您也和我一樣期待下一篇文章。
對於這篇文章有什麼想法呢?喜歡😻、留言🙋♂️或者分享🙌